全讯网-皇冠网

近日，北京理工大學(xué)物理學(xué)院姚裕貴教授、周迪研究員團隊在《Nature Communications》發(fā)表題為 “Topological invariant and anomalous edge modes of strongly nonlinear systems” 的文章。團隊通過數(shù)學(xué)推導(dǎo)，研究了廣義強非線性系統(tǒng)，在非線性波中提出貝里相位的合理定義，并嚴(yán)格證明其量子化條件。作者通過理論計算和數(shù)值模擬，驗證了非線性拓?fù)淠５姆€(wěn)定性，將 “體邊對應(yīng)關(guān)系”推廣到廣義強非線性系統(tǒng)中。北京理工大學(xué)周迪研究員為論文的第一作者，周迪研究員和姚裕貴教授為論文的共同通訊作者。論文的合作者包括佐治亞理工大學(xué)的D. Zeb Rocklin教授和Michael J. Leamy教授。

拓?fù)淠軒Ю碚摰慕⒋偈埂拔镔|(zhì)拓?fù)湎唷边@一領(lǐng)域的迅猛發(fā)展。具有拓?fù)湫再|(zhì)的電子系統(tǒng)會表現(xiàn)出自然界材料所不具備的超常輸運性和穩(wěn)定性。相比量子系統(tǒng)而言，經(jīng)典系統(tǒng)的物理性質(zhì)更直觀、更容易應(yīng)用于實際生活中。這些基于力、電、聲、光的特殊物性所構(gòu)造的 “拓?fù)涑牧稀保纬闪水?dāng)前物理研究的新興前沿領(lǐng)域。這些超材料的研究為拓?fù)浣?jīng)典波的操縱調(diào)控，以及拓?fù)湮锢淼奶骄坷斫猓峁┝巳缕脚_。

近年來，在以非線性光學(xué)為代表的一系列經(jīng)典拓?fù)湎到y(tǒng)中，人們發(fā)現(xiàn)了諸多非線性材料的新奇物性。例如，振幅調(diào)控的拓?fù)鋺B(tài)頻率、振幅導(dǎo)致的拓?fù)湎嘧儭⑼負(fù)湫盘柕墓舱裢健⒁约胺蔷€性自誘導(dǎo)拓?fù)鋺B(tài)等。然而，當(dāng)前的大部分研究僅限于 “克爾類型”（Kerr-like）的非線性系統(tǒng)，和弱非線性系統(tǒng)。事實上，自然界中的大多數(shù)非線性系統(tǒng)非常復(fù)雜，其中的非線性模態(tài)缺乏深入認(rèn)知，從而導(dǎo)致它們的拓?fù)洳蛔兞亢屯負(fù)湎酂o法定量刻畫。日常生活中，復(fù)雜的非線性相互作用包括：非線性電路、彈性力學(xué)、流體動力學(xué)、生物進化過程，以及考慮了二次諧波的非線性光學(xué)問題。為了理解這些廣義非線性作用所導(dǎo)致的拓?fù)湮镄裕覀冃枰⒁惶赘者m的拓?fù)淅碚摗Ｋ鼘τ谕負(fù)涑牧系脑O(shè)計，以及非線性新奇物性的研究，具有重要的科學(xué)意義。

本文通過研究廣義非線性模型，在非線性振蕩模式中提出貝里相位的概念，推導(dǎo)了貝里相位的數(shù)學(xué)形式。作者證明，在反射對稱性約束下，貝里相位能夠被量子化，進而刻畫廣義非線性系統(tǒng)的拓?fù)湎唷Ｔ摴ぷ鬟M一步將自誘導(dǎo)拓?fù)鋺B(tài)推廣到了強非線性區(qū)域中。與線性拓?fù)淠２煌@些拓?fù)淠５恼穹蛇吔缢p到一個零平臺，并且該平臺的幅值由系統(tǒng)非線性作用的穩(wěn)定不動點所決定。

通過這一工作，作者證明了 “拓?fù)浔Ｗo”的概念普遍存在于非線性系統(tǒng)中，而不局限于克爾非線性與弱非線性系統(tǒng)。本文為拓?fù)涑牧系脑O(shè)計和非線性拓?fù)湮镄缘难芯刻峁┝死碚摶A(chǔ)。相關(guān)工作發(fā)表在Nature Communications 13, 3379 (2022)。

該工作得到國家自然科學(xué)基金委（11734003,和12061131002）科技部國家重點研發(fā)計劃（2020YFA0308800）、中國科學(xué)院戰(zhàn)略性先導(dǎo)科技專項資助（XDB30000000）等項目的支持。

不同振幅的外界信號激勵下，同樣的非線性系統(tǒng)會表現(xiàn)出截然不同的拓?fù)湮镄浴D1和圖2分表描述了兩種非線性拓?fù)潴w系。（圖1）小振幅外界信號驅(qū)動下，體系處于非線性拓?fù)湎唷６笳穹饨珧?qū)動下，體系處于拓?fù)淦接瓜唷＃▓D2）小振幅驅(qū)動下，體系處于平庸相。大振幅激勵下，體系處于拓?fù)湎唷?/p>

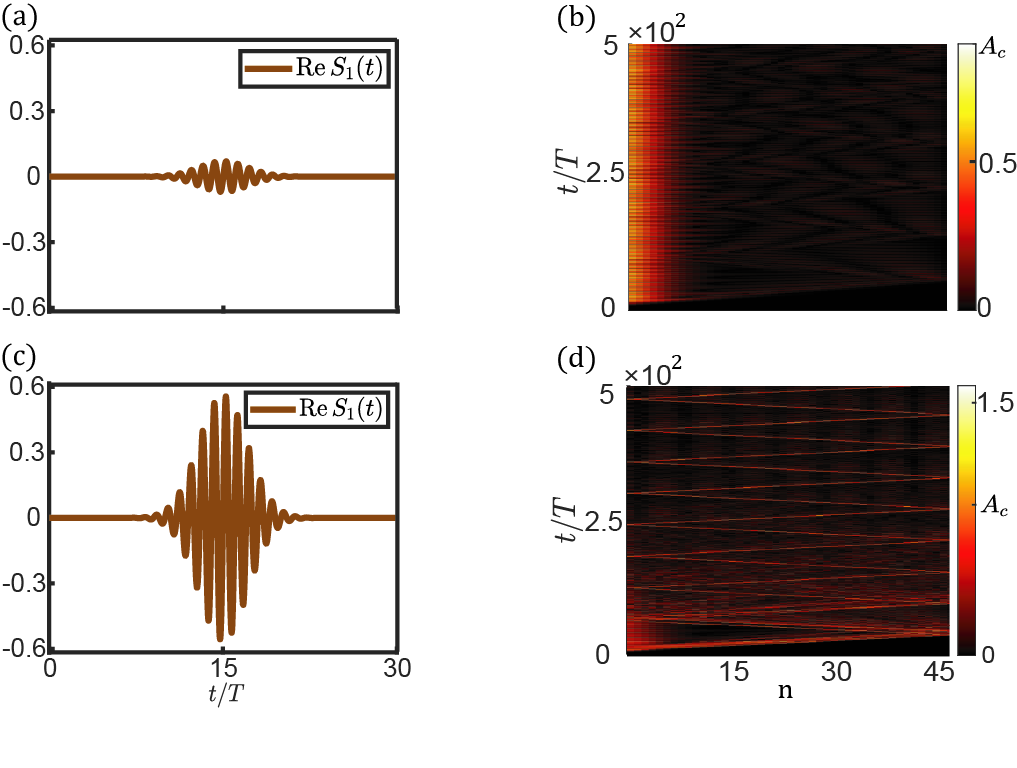
圖1 小振幅拓?fù)洹⒋笳穹接沟姆蔷€性系統(tǒng)。(a, b) 小振幅激勵信號下，系統(tǒng)表現(xiàn)出拓?fù)溥吘墤B(tài)響應(yīng)。(c, d) 大振幅激勵信號下，系統(tǒng)表現(xiàn)出體模響應(yīng)。

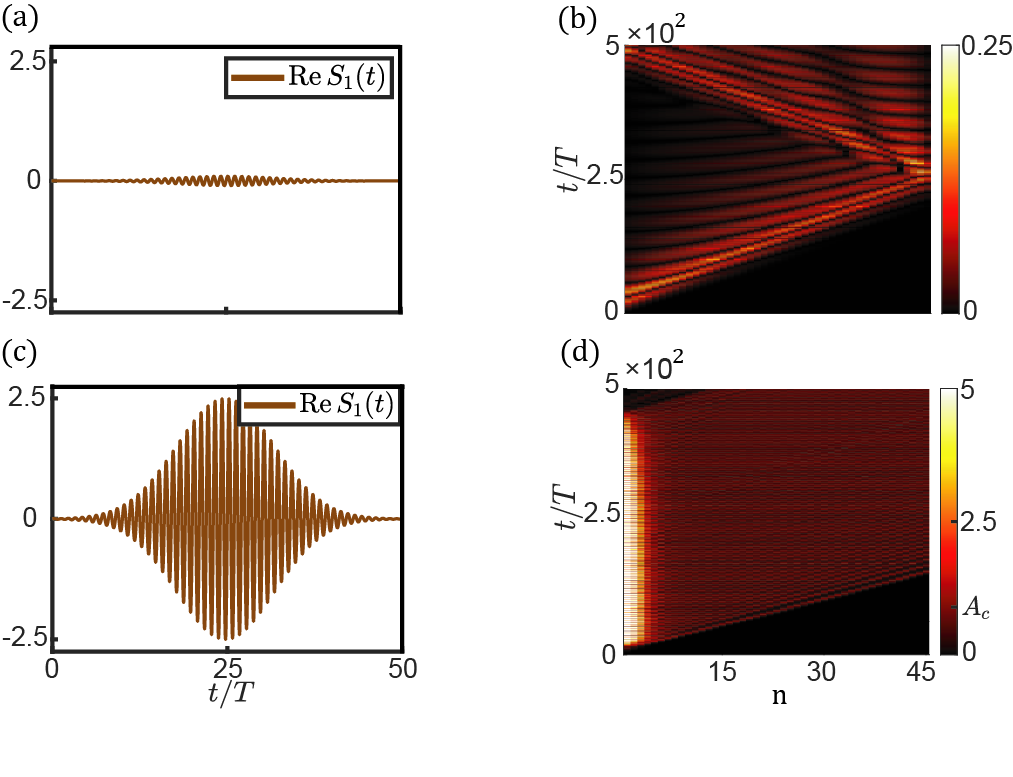
圖2 小振幅平庸、大振幅拓?fù)涞姆蔷€性系統(tǒng)。(a, b) 小振幅激勵信號下，系統(tǒng)表現(xiàn)出體模響應(yīng)。(c, d) 大振幅激勵信號下，系統(tǒng)表現(xiàn)出拓?fù)溥吘墤B(tài)響應(yīng)。

原文鏈接：https://www.nature.com/articles/s41467-022-31084-y